NÙMEROS COMPLEJOS.
Ecuaciones sin soluciòn real.
No existe un número real x que satisfaga la ecuación polinómica x2+1 = 0 . Para resolver este tipo de ecuaciones, es necesario introducir los números complejos.
Se define un número complejo, z , mediante la siguiente expresión:
z = a + bi
donde a y b son una pareja cualquiera de números reales. Llamamos i a la unidad imaginaria compleja. Definimos i de la siguiente manera:
i = √¯-1 ; i2 = − 1.
Si z = a + bi , a se llama la parte real de z y b el coeficiente de la parte imaginaria de z y se denominan mediante a = ℜ(z) y b = ℑ(z) , respectivamente. El símbolo z , que puede representar cualquier elemento del conjunto de números complejos, es llamado una variable compleja.
El término número complejo describe la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i. Los números complejos se utilizan en todos los campos de las matemáticas, en muchos de la física (y notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.
En matemáticas, los números constituyen un cuerpo y, en general, se consideran como puntos del plano: el plano complejo. La propiedad más importante que caracteriza a los números complejos es el teorema fundamental del álgebra, que afirma que cualquier ecuación algebraica de grado n tiene exactamente n soluciones complejas.
Los números complejos son una extensión de los números reales, cumpliéndose que  . Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales.
. Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales.
 . Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales.
. Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales. Los números complejos son la herramienta de trabajo del álgebra ordinaria, llamada álgebra de los números complejos, así como de ramas de las matemáticas puras y aplicadas como variable compleja, aerodinámica y electromagnetismo entre otras de gran importancia.
Contienen a los números reales y los imaginarios puros y constituyen una de las construcciones teóricas más importantes de la inteligencia humana. Los análisis del cálculo diferencial e integral con números complejos reciben el nombre de variable compleja o análisis complejo.
Definiciones:
Definiremos cada complejo z como un par ordenado de números reales (a, b). Al primer componente (que llamaremos a) se le llama parte real y al segundo (que llamaremos b), parte imaginaria. Se denomina número imaginario puro a aquel que esta compuesto sólo por la parte imaginaria, es decir, aquel en el que a = 0 .
Representación binómica de un nùmero complejo.

Un número complejo se representa en forma binomial como:
La parte real del número complejo y la parte imaginaria, se pueden expresar de varias maneras, como se muestra a continuación:
Valor absoluto o módulo de un número complejo
El valor absoluto, módulo o magnitud de un número complejo z viene dado por la siguiente expresión:
Si pensamos en las coordenadas cartesianas del número complejo z como algún punto en el plano; podemos ver, por el teorema de Pitágoras, que el valor absoluto de un número complejo coincide con la distancia euclídea desde el origen del plano a dicho punto.
Argumento
El argumento o fase de un número complejo z viene dado por la siguiente expresión:
donde arctan() es la función arcotangente.
Conjugado de un número complejo
Dos binomios se llaman conjugados si solo difieren en su signo central, por ejemplo, los dos binomios:
3m - 1 y 3m + 1 son conjugados.
El conjugado de un complejo z (denotado como  ó
ó  ) es un nuevo número complejo, definido así:
) es un nuevo número complejo, definido así:
 ó
ó  ) es un nuevo número complejo, definido así:
) es un nuevo número complejo, definido así: Se observa que ambos solo difieren en el signo de la parte imaginaria.
Operaciones con nùmeros complejos
Suma
Para sumar números complejos, se siguen las normas básicas de la aritmética, sumando los reales con los reales y los imaginarios con los imaginarios:
Ejemplo de suma:
- (4 + 2i) + (3 + 2i) = 4 + 2i + 3 + 2i = 4 + 3 + 2i + 2i = (4 + 3) + (2 + 2)i =
el resultado es 7 + 4i
Resta
Al igual que en la suma, se opera como con los números reales ordinarios, teniendo en cuenta que se le cambia el signo al sustraendo:
Otro ejemplo: (6-4i) - (6+5i) = 6-4i-6-5i = (6-6)+(-4i-5i) = (6-6)+(-4 -5)i = 0 - 9i.
Multiplicación
Para multiplicar dos números complejos, se multiplica cada término del primero por los dos del segundo, con lo que obtenemos 4 términos:
Obsérvese que el término bdi2 pasa a ser − bd. Eso es porque i2 = − 1.
Ejemplo:
División
La división de números complejos requiere un mayor trabajo que la multiplicación y partimos de un artificio previo, basado en que el producto de un numero complejo por su conjugado da como resultado un número real:
Para realizar la división de dos números complejos, multiplicamos y dividimos por el conjugado del denominador:

- Ejemplo:
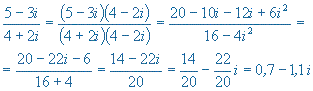
Potencias
Para elevar un número complejo a un exponente entero, se aplican las identidades notables. Se debe tener en cuenta la igualdad i2 = − 1:

- Forma polar y trigonomètrica.
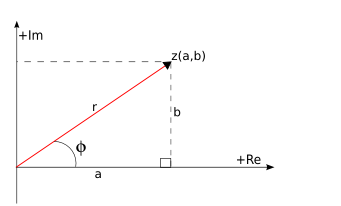
Módulo y argumento de un número complejo
Forma polar de un número complejo
La forma polar del número complejo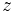 , se designa
, se designa 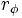 , siendo
, siendo 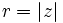 y
y 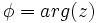
Paso de forma binómica a polar
Dado un número complejo 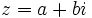 su forma polar
su forma polar 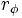 se obtiene de la siguiente manera:
se obtiene de la siguiente manera:
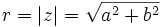 (por el teorema de Pitágoras)
(por el teorema de Pitágoras)
 Ejemplo: Paso de forma binómica a polar
Ejemplo: Paso de forma binómica a polar
- Pasa a forma polar el número complejo
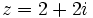
- Calculamos el módulo:
- Calculamos el argumento:
- Por tanto, su forma polar es:
Paso de forma polar a binómica
- Dado un número complejo
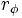 , su forma binómica
, su forma binómica  se obtiene de la siguiente manera:
se obtiene de la siguiente manera:
- a = r cos φ
- b = r sen φ
- Pasa a forma binómica el número complejo
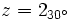
- Calculamos la parte real:
- Calculamos su parte imaginaria:
- Por tanto, su forma binómica es:
Forma trigonométrica de un número complejo
- Según lo visto en el apartado anterior:
- Z = a + bi = r cos φ + r sen φ. i = r ( cos φ + i sen φ )
Ejemplo: Paso de forma polar a binómicaSe llama forma trigonométrica de un número complejo, a la expresiónZ = r ( cos φ + i sen φ ).Ejemplo: Forma trigonométrica de un complejo
- Pasa a forma trigonométrica el número complejo
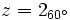
Tan sólo hay que aplicar la fórmula: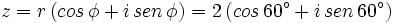
- Operaciones en forma polar
Multiplicación de números complejos en forma polar
El producto de dos numeros complejos en forma polar es otro complejo en forma polar cuyo módulo es el producto de los módulos y el argumento la suma de los argumentos de los respectivos complejos.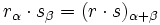 Ejemplo:
Ejemplo: 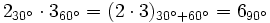
Potencias de números complejos en forma polar
La potencia n-ésima de un compejo se obtiene de la siguiente manera: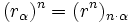 Ejemplo:
Ejemplo: 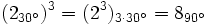
Fórmula de De Moivre
La utilizaremos para elevar a una potencia un complejo escrito en forma trigonométrica: Zn = rn ( cos nφ + i sen nφ )División de números complejos en forma polar
La división de dos numeros complejos en forma polar es otro complejo en forma polar cuyo módulo es el cociente de los módulos y el argumento la diferencia de los argumentos de los respectivos complejos.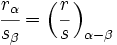 Ejemplo: Dividir
Ejemplo: Dividir 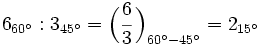
Radicación de números complejos en forma polar
Un número complejo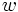 es una raíz n-ésima de otro complejo
es una raíz n-ésima de otro complejo 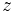 si se cumple que
si se cumple que 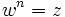 Un número complejo
Un número complejo 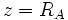 tiene exactamente n raíces n-ésimas
tiene exactamente n raíces n-ésimas 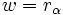 , que se obtienen de la siguiente manera:
, que se obtienen de la siguiente manera: ![r_\alpha : \begin{cases} r=\sqrt[n]{R} \\ \alpha=\cfrac{A+2k \pi}{n}\, , \quad k=0,1,\cdots,(n-1) \end{cases}](http://maralboran.org/wikipedia/images/math/4/a/5/4a5dd4f3f68e14f0c8013ccc27085e5e.png) Ejemplo: Raíces de un complejo Calcula:
Ejemplo: Raíces de un complejo Calcula: ![\sqrt[3]{1+i}](http://maralboran.org/wikipedia/images/math/8/8/3/883e0a5f87d5879d879d48e3bbe5789d.png) Primero pasamos el complejo
Primero pasamos el complejo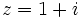 a forma polar: Así,
a forma polar: Así,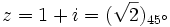 Ahora procedemos a calcular sus 3 raíces cubicas:
Ahora procedemos a calcular sus 3 raíces cubicas:![\sqrt[3]{(\sqrt{2})_{45^\circ}}=r_\alpha](http://maralboran.org/wikipedia/images/math/c/5/e/c5e849c7713f59a373e993c0d21a8bd5.png) , siendo
, siendo ![\begin{cases} r=\sqrt[3]{\sqrt{2}} \\ \alpha=\cfrac{45^\circ +2k \pi}{3}\, , \quad k=0,1,2 \end{cases}](http://maralboran.org/wikipedia/images/math/e/3/3/e338be4b3b0010eb3dd1abb6ea6669f0.png) De donde
De donde![r_\alpha : \begin{cases} r=\sqrt[6]{2} \\ \alpha= 15^\circ \, , \quad 135^\circ \, , \quad 257^\circ \end{cases}](http://maralboran.org/wikipedia/images/math/d/9/7/d978739b21c71e554a372161eb06a8b7.png) Soluciones:
Soluciones:












 y el origen
y el origen 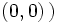 . Se designa por
. Se designa por 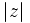 .
.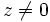 ), es el ángulo que forma el vector con el eje X . Se designa por
), es el ángulo que forma el vector con el eje X . Se designa por 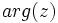 . (Si
. (Si 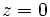 , su argumento es 0).
, su argumento es 0).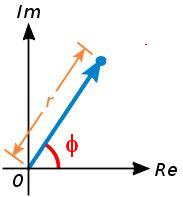
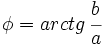
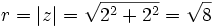
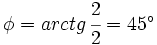

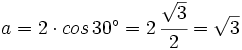

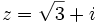
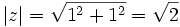
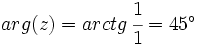
![(\sqrt[6]{2})_{15^\circ} \, , \quad (\sqrt[6]{2})_{135^\circ} \, , \quad (\sqrt[6]{2})_{257^\circ}](http://maralboran.org/wikipedia/images/math/a/d/b/adb33551ba73519cab6c3b98e938918b.png)