COMBINATORIA
Concepto o definición:
La combinatoria es una rama de la matemática perteneciente al área de matemáticas discretas que estudia la enumeración, construcción y existencia de propiedades de configuraciones que satisfacen ciertas condiciones establecidas.
Combinatoria enumerativa
La combinatoria enumerativa o enumeración estudia los métodos para contar (enumerar) las distintas configuraciones de los elementos de un conjunto que cumplan ciertos criterios especificados.
Esta fue una de las primeras áreas de la combinatoria en ser desarrollada, y como otras áreas más recientes se estudian sólo en cursos especializados, es común que se haga referencia a esta subárea cuando se menciona combinatoria en entornos escolares.
- Ejemplo:
Considérese el conjunto S = {A,E,I,O,U}. Podemos imaginar que estos elementos corresponden a tarjetas dentro de un sombrero.
Un primer problema podría consistir en hallar el número de formas diferentes en que podemos sacar las tarjetas una después de otra (es decir, el número de permutaciones del conjunto).Por ejemplo, dos formas distintas podrían ser: EIAOU o OUAIE.
Después, se puede preguntar por el número de formas en que se puede sacar sólo 3 tarjetas del sombrero (es decir, el número de 3-permutaciones del conjunto).En este caso, ejemplos pueden ser IOU, AEI o EAI.
También se puede preguntar sobre cuáles son los posibles grupos de 3 tarjetas que se pueden extraer, sin dar consideración al orden en que salen (en otras palabras, el valor de un coeficiente binomial).Aquí, consideraríamos AOU y UAO como un mismo resultado.
Otro problema consiste en hallar el número de formas en que pueden salir 5 tarjetas, una tras otra, pero en cada momento se regresa la tarjeta escogida al sombrero. En este problema los resultados posibles podrían ser EIOUO, IAOEU o IEAEE.
La combinatoria enumerativa estudia las técnicas y métodos que permiten resolver los problemas anteriores, así como otros más complejos, cuando el número de elementos del conjunto es arbitrario. De esta forma, en el primer ejemplo la generalización correspondiente es determinar el número de formas en que se pueden ordenar todos los elementos de un conjunto con n elementos, siendo la respuesta el factorial de n.
Números combinatorios.
Factorial de un número natural
Para todo entero positivo n, el factorial de n o n factorial se define como el producto de todos los números enteros positivos desde 1 hasta n. Es decir
La multiplicación anterior se puede simbolizar también como:
En general:
La operación de factorial aparece en muchas áreas de las matemáticas, particularmente en combinatoria y análisis matemático. De manera fundamental, el factorial de n representa el número de formas distintas de ordenar n objetos distintos. Este hecho ha sido conocido desde hace varios siglos, en el s. XII por los estudiosos indios. La notación actual n! fue usada por primera vez por Christian Kramp en 1803.
Cero factorial
La definición indicada de factorial es válida para números positivos. Es posible extender la definición a otros contextos introduciendo conceptos más sofisticados, en especial es posible definirla para cualquier número real excepto para los números enteros negativos y para cualquier número complejo exceptuando de nuevo los números enteros negativos.
Una extensión común, sin embargo, es la definición de factorial de cero. De acuerdo con la convención matemática de producto vacío, el valor de 0! debe definirse como 0!=1.
Es posible, sin embargo, dar un argumento intuitivo para justificar la elección, como sigue:
Para cada número entero positivo n mayor que 1, es posible determinar el valor del factorial anterior mediante el uso de la siguiente identidad:
,
válida para todo número mayor o igual que 1.
Así, si se conoce que 5! es 120, entonces 4! es 24 porque
4!=,
y por tanto 3! debe ser necesariamente 6 puesto que
3!=.
El mismo proceso justifica el valor de 2! = 2 y 1!=1 ya que
Si aplicamos la misma regla para el caso extremo en que n'=1 tendríamos que 0! corresponde a
Aunque el argumento puede resultar convincente, es importante tener en cuenta que no es más que un argumento informal y que la razón real por la cual se toma la convención de 0! = 1 es por ser un caso especial de la convención de producto vacío usada en muchas otras ramas de las matemáticas.
Coeficiente binomial
Los coeficientes binomiales, números combinatorios o combinaciones son números estudiados en combinatoria que corresponden al número de formas en que se pueden extraer subconjuntos a partir de un conjunto dado. Sin embargo, dependiendo del enfoque que tenga la exposición, se pueden usar otras definiciones equivalentes.
Definición combinatoria
Se tiene un conjunto con 6 objetos diferentes {A,B,C,D,E,F}, de los cuales se desea escoger 2 (sin importar el orden de elección). Existen 15 formas de efectuar tal elección:
El número de formas de escoger k elementos a partir de un conjunto de n, puede denotarse de varias formas:
 ,
,  ,
,  , o
, o  .
. Así, en el ejemplo anterior se tiene entonces que C(6,2)=15, puesto que hay 15 formas de escoger 2 objetos a partir de un conjunto con 6 elementos.
Los números C(n,k) se conocen como «coeficientes binomiales», pero es frecuente referirse a ellos como «combinaciones de n en k», o simplemente «n en k». Por tanto, la primera definición es:
El coeficiente binomial  es el número de subconjuntos de k elementos escogidos de un conjunto con n elementos.
es el número de subconjuntos de k elementos escogidos de un conjunto con n elementos.
 es el número de subconjuntos de k elementos escogidos de un conjunto con n elementos.
es el número de subconjuntos de k elementos escogidos de un conjunto con n elementos. Definición algebraica
La definición no permite calcular el valor de los coeficientes binomiales, salvo listando los subconjuntos y contándolos. Sin embargo, existe una fórmula explícita que nos proporciona el valor de C(n,k).
Supongamos que el conjunto original tiene 5 elementos,{A,B,C,D,E}, de los cuales se deben escoger 3. Al momento de escoger el primero, se tiene 5 opciones disponibles, pero una vez fijo el primero, sólo hay 4 opciones para el segundo, y por tanto sólo 3 opciones para el último (pues no se puede repetir los escogidos en los primeros 2 pasos). De este modo, la selección puede hacerse de 5×4×3=60 formas.
Sin embargo, en tal conteo, el orden en que se escogen los elementos hace diferencia. Por ejemplo, tomar C, luego B, luego E, es una selección diferente de tomar B, luego C y luego E. Pero en la definición de coeficiente binomial, no importa el orden en que se eligen los objetos, únicamente cuáles se escogen. Por tanto, las elecciones BCE, BEC, CEB, CBE, ECB y EBC son todas equivalentes. Del mismo modo, las elecciones ABC, ACB, BCA, BAC, CAB y CBA son equivalentes, y así para cualquier terna de letras.
De esta forma, el resultado obtenido (60) no es la cantidad de subconjuntos de 3 elementos de {A,B,C,D,E}, sino que cada subconjunto está contado 6 veces, por lo que la cantidad de subconjuntos es realmente 60/6 = 10.
El argumento presentado para el ejemplo puede generalizarse de la siguiente forma. Si se tiene un conjunto con n elementos, de los cuales se van a escoger k de ellos, la elección (ordenada) puede hacerse de
- n × (n-1) × (n-2) ×... × (n-k+1)
ya que en el primer paso se tienen n opciones, en el segundo se tienen n-1, en el tercero n-2, y así sucesivamente, terminando en el paso k que tendrá n-k+1 opciones.
Ahora, hay que dividir el producto anterior entre el número de selecciones «equivalentes». Pero si se tiene k objetos, hay k! formas de permutarlos, es decir, k! formas de listarlos en distinto orden. Recordemos que k! se lee k-factorial y es igual a
- k! = 1×2×3×...× k
Concluimos que el número de subconjuntos con k elementos, escogidos de un conjunto con n elementos es
 .
.
Multiplicando el numerador y el denominador de la fracción por 1×2×3×···×(n-k)
La expresión anterior puede escribirse de forma más compacta usando factoriales, expresión que es usada en ocasiones como la definición misma de coeficiente binomial (sobre todo en textos elementales que no explican el origen combinatorio de la misma):
Binomio de Newton. El teorema de binomio y coeficientes binomiales Finalmente, existe una tercera forma de definir los coeficientes binomiales, la cual da origen a su nombre. Sin embargo, esta definición obscurece el significado combinatorio de los números, pues la equivalencia con las definiciones anteriores no es evidente. Por ejemplo, si desarrollamos (x+y)3 obtenemos:  Para ilustrar la equivalencia entre esta definición y la anterior, consideremos un ejemplo con n=3,k=2. Podemos pensar que los factores de (x+y)³=(x+y)(x+y)(x+y) están coloreados de azul, rojo y verde respectivamente. Por un lado, se sabe que (x+y)³ = x³+3x²y+3xy²+y³, por lo que el coeficiente de x²y es 3. Por otro lado, al desarrollar los factores, aparecerá un término x²y cada vez que se elija dos colores para x (dejando el color restante para y). El número de formas de escoger 2 colores entre 3 posibles opciones es precisamente C(3,2), como se estableció con anterioridad. La conclusión es que el coeficiente de x²y es necesariamente C(3,2). Para el caso general, se puede imaginar que los n factores de (x+y)n han sido coloreados con diferentes colores, por lo que el coeficiente de xkyn-k será igual al número de formas de escoger k colores para asignarlos a la variable x (dejando los n-k colores restantes para y). El número de formas para escoger k colores entre n posibles opciones es C(n,k), con lo que se termina la prueba. La afirmación de que esta definición es equivalente a las anteriores se conoce como teorema binomial o teorema de Newton, quien dio una prueba de una versión general del resultado. Sin embargo, la forma de calcular los coeficientes era conocida por diversas culturas con muchos siglos de anticipación. En contextos más técnicos, suele usarse una forma diferente de expresar el teorema de Newton mediante el uso de sumatorios:
Esta fórmula se generaliza para más de dos sumandos de la siguiente manera:
donde  es un coeficiente multinomial que se define: es un coeficiente multinomial que se define:  . Los coeficientes multinomiales también tienen definición combinatoria. Puesto que n no es más que la suma de n1, n2,... y nr, también se emplean notaciones en las que n, no aparece, como . Los coeficientes multinomiales también tienen definición combinatoria. Puesto que n no es más que la suma de n1, n2,... y nr, también se emplean notaciones en las que n, no aparece, como  . Otras notaciones son . Otras notaciones son  ó ó  Variaciones ordinarias y con repetición. Variaciones sin repetición (ordinarias)
Como el primero de los elementos puede ser cualquiera de los m disponibles, el segundo cualquiera de los (m – 1) restantes, el tercero cualquiera de los (m – 2) que quedan y así sucesivamente, aplicando el principio de la multiplicación se obtiene:

|

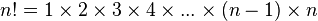





 obtenido al desarrollar
obtenido al desarrollar 
 .
.  ,
, m), son los distintos grupos de n elementos no repetidos que se pueden formar, escogidos de entre los m elementos posibles, de forma que en cada grupo haya algún elemento distinto, o tenga los mismos elementos que otro grupo, pero colocados en distinto orden. Cada uno de los posibles grupos es una variación. Se representa por
m), son los distintos grupos de n elementos no repetidos que se pueden formar, escogidos de entre los m elementos posibles, de forma que en cada grupo haya algún elemento distinto, o tenga los mismos elementos que otro grupo, pero colocados en distinto orden. Cada uno de los posibles grupos es una variación. Se representa por  .
.
 .
.




 y su valor viene dado por:
y su valor viene dado por: 
