Unidad no. 8: Derivadas.

DERIVADA DE UNA FUNCIÓN.

Tasa de variaciòn media (T.V.M).

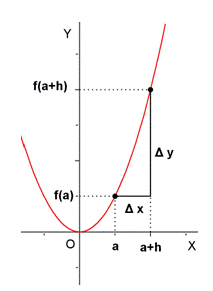
Figura: El punto b = a + h.

Para medir el crecimiento de una función en un intervalo [a,b], se utiliza la tasa de variación media (T.V.M.), que se define como el cociente de la variación de y entre la variación de x:

$T.V.M._f \,[a,b]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(b)-f(a)}{b-a}$

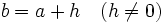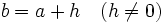Si llamamos $b=a+h \quad (h \ne 0)$ , la expresión anterior queda como sigue:

$T.V.M._f \,[a,a+h]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=\cfrac{f(a+h)-f(a)}{h}$

La T.V.M. de una función en un intervalo [a,b] es igual a la pendiente de la recta secante a la gráfica de la función en puntos de abcisas a y b.

Observa la figura de arriba. Por la definición de T.V.M. y teniendo en cuenta que la tangente de un ángulo es el cociente entre el cateto opuesto y el cateto adyacente, tenemos:

$T.V.M._f \,[a,b]=\cfrac{\mathcal{4}y}{\mathcal{4}x}=tg\, \alpha=m$

donde $m\,$ es la pendiente de la recta r.

El límite de la tasa de variaciòn media (TVM) cuando el incremento de la variable independiente (ΔX) tiende a cero, es a lo que llamamos Tasa de Variaciòn instantànea, que origina el concepto de derivada de una funciòn.

Concepto de derivada de una función.

En matemáticas, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se toma cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.

Un ejemplo habitual aparece al estudiar el movimiento: si una función representa la posición de un objeto con respecto al tiempo, su derivada es la velocidad de dicho objeto. Un avión que realice un vuelo transatlántico de 4500 km en entre las 12:00 y las 18:00, viaja a una velocidad media de 750 km/h. Sin embargo, puede estar viajando a velocidades mayores o menores en distintos tramos de la ruta. En particular, si entre las 15:00 y las 15:30 recorre 400 km, su velocidad media en ese tramo es de 800 km/h. Para conocer su velocidad instantánea a las 15:20, por ejemplo, es necesario calcular la velocidad media en intervalos de tiempo cada vez menores alrededor de esta hora: entre las 15:15 y las 15:25, entre las 15:19 y las 15:21, etc.

El valor de la derivada de una función en un punto puede interpretase geométricamente, ya que se corresponde con pendiente de la recta tangente a la gráfica de la función en dicho punto. La recta tangente es a su vez la gráfica de la mejor aproximación lineal de la función alrededor de dicho punto. La noción de derivada puede generalizarse para el caso de funciones de más de una variable con la derivada parcial y el diferencial.

La derivada de una función f en un punto x se denota como f′(x). La función cuyo valor en cada punto x es esta derivada es la llamada función derivada de f, denotada por f'. El proceso de encontrar la derivada de una función se denomina diferenciación, y es una de las herramientas principales en el área de las matemáticas conocida como cálculo.

Definición analítica de derivada como un límite

En terminología clásica, la diferenciación manifiesta el coeficiente en que una cantidad $y\,$ cambia a consecuencia de un cambio en otra cantidad $x\,$ .

En matemáticas, coeficiente es un factor multiplicativo que pertenece a cierto objeto como una variable, un vector unitario, una función base, etc.

En física, coeficiente es una expresión numérica que mediante alguna fórmula determina las características o propiedades de un cuerpo.

En nuestro caso, observando la gráfica de arriba, el coeficiente del que hablamos vendría representado en el punto $P\,$ de la función por el resultado de la división representada por la relación $\frac{dy}{dx}$ , que como puede comprobarse en la gráfica, es un valor que se mantiene constante a lo largo de la línea recta azul que representa la tangente en el punto $P\,$ de la función. Esto es fácil de entender puesto que el tríangulo rectángulo formado en la gráfica con vértice en el punto $P\,$ , por mucho que lo dibujemos más grande, al ser una figura proporcional el resultado de $\frac{dy}{dx}$ es siempre el mismo.

Esta noción constituye la aproximación más veloz a la derivada, puesto que el acercamiento a la pendiente de la recta tangente es tanto por la derecha como por la izquierda de manera simultánea.

Considerando la función f definida en el intervalo abierto I y un punto a fijo en I, se tiene que la derivada de la función f en el punto $a\,$ se define como sigue:

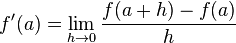$f'(a)=\lim_{h\rightarrow0} \frac{f(a + h) - f(a)}{h}$ ,

si este límite existe, de lo contrario,

f'

, la derivada, no está definida. Esta última expresión coincide con la velocidad instantánea del movimiento continuo uniforme acelerado en cinemática.

Aunque podrían calcularse todas las derivadas empleando la definición de derivada como un límite, existen reglas bien establecidas, conocidas como teoremas para el cálculo de derivadas, las cuales permiten calcular la derivada de muchas funciones de acuerdo a su forma sin tener que calcular forzosamente el límite. Tales reglas son consecuencia directa de la definición de derivada y de reglas previas, como puede apreciarse en todo buen texto de cálculo infinitesimal.

También puede definirse alternativamente la derivada de una función en cualquier punto de su dominio de la siguiente manera:

$f'(a)=\lim_{x\rightarrow a} \frac{f(x) - f(a)}{x - a}$ ,

La cual representa un acercamiento de la pendiente de la secante a la pendiente de la tangente ya sea por la derecha o por la izquierda según el signo de $a\,$ . El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.

No obstante su aparente diferencia, el cálculo de la derivada por definición con cualquiera de los límites anteriormente expresados, proporciona siempre el mismo resultado.

Derivadas de las operaciones con funciones.

Lista de derivadas de funciones elementales

En las fórmulas siguientes se considera que $x,a,b,k \in \mathbb{R}, n \in \mathbb{N}$ :

$f\left(x\right) = a$	$f'\left(x\right) = 0$
$f\left(x\right) = x$	$f'\left(x\right) = 1$
$f\left(x\right) = ax$	$f'\left(x\right) = a$
$f\left(x\right) = ax + b$	$f'\left(x\right) = a$
$f\left(x\right) = x^n$	$f'\left(x\right) = nx^{n-1}$
$f\left(x\right) = \sqrt{x}$	$f'\left(x\right) = \frac{1}{2\sqrt{x}}$
$f\left(x\right) = e^x$	$f'\left(x\right) = e^x$
$f\left(x\right) = \ln(x)$	$f'\left(x\right) = \frac{1}{x}$
$f\left(x\right) = a^x (a >0)$	$f'\left(x\right) = a^x \ln(a)$
$f\left(x\right) = \log_{b}(x)$	$f'\left(x\right) = \frac{1}{x\ln(b)}$
$f\left(x\right) = \frac{1}{x^n} = x^{-n}$	$f'\left(x\right) = -nx^{-n-1} = \frac{-n}{x^{n+1}}$
$f\left(x\right) = \operatorname{sen}(x)$	$f'\left(x\right) = \cos(x)$
$f\left(x\right) = \cos(x)$	$f'\left(x\right) = -\operatorname{sen}(x)$
$f\left(x\right) = \tan(x)$	$f'\left(x\right)=\sec^2(x)=\frac{1}{cos^2(x)}=1+\tan^2(x)$
$f\left(x\right) = \csc(x)$	$f'\left(x\right) = -\csc(x)\cot(x)$
$f\left(x\right) = \sec(x)$	$f'\left(x\right) = \sec(x)\tan(x)$
$f\left(x\right) = \cot(x)$	$f'\left(x\right) = -\csc^2(x)$
$f\left(x\right) = \operatorname{arcsen}(x)$	$f'\left(x\right) = \frac{1}{\sqrt{1-x^2}}$
$f\left(x\right) = \arccos(x)$	$f'\left(x\right) = \frac{-1}{\sqrt{1-x^2}}$
$f\left(x\right) = \arctan(x)$	$f'\left(x\right) = \frac{1}{1+x^2}$
$f\left(x\right) = g(x) \pm h(x)$	$f'\left(x\right) = g'(x) \pm h'(x)$
$f\left(x\right) = g(x) \cdot h(x)$	$f'\left(x\right) = g'(x) \cdot h(x) + g(x) \cdot h'(x)$
$f\left(x\right) = k \cdot g(x)$	$f'\left(x\right) = k \cdot g'(x)$
$f\left(x\right) = \frac{g(x)}{h(x)}$	$f'\left(x\right) = \frac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{h^2(x)}$
$f\left(x\right) = g\left(x\right)^{h\left(x\right)}$	$f'\left(x\right) = h\left(x\right) \cdot g'\left(x\right) \cdot g\left(x\right)^{\left(h\left(x\right)-1\right)} + g\left(x\right)^{h\left(x\right)} \cdot h'\left(x\right) \cdot ln\left(g\left(x\right)\right)$
$f\left(x\right) = g \circ h = g(h(x))$	$f'\left(x\right) = (g'\circ h) \cdot h' = g'(h(x)) \cdot h'(x)$ (regla de la cadena)

Ejercicios resueltos.

Ejemplo #1

Sea $f \,$ la función $f(x)=2x^3-9x^2-24x+51 \,$ , definida sobre el conjunto de los números reales (denotado por $\mathbb R \,$ ). Para conocer sus variaciones se observa su derivada:

$f^\prime(x)=6x^2-18x-24$

Para encontrar el signo de $f^\prime(x)$ , se tiene que factorizar:

$\begin{array}{rcl}f^\prime(x)&=&6(x^2-3x-4)\\&=&6(x+1)(x-4)\end{array}$

lo anterior que se hace resolviendo una ecuación de segundo grado.

También se observa su segunda derivada:

f''(x) = 12 x - 18

Dado que $f'(-1)=0\,$ y $f''(-1)<0\,$ entonces $f\,$ tiene un máximo local en -1 y su valor es $f(-1)=64\,$ .

Dado que $f'(4)=0\,$ y $f''(4)>0\,$ entonces $f\,$ tiene un mínimo local en 4 y su valor es $f(4)=-61\,$ .

Nótese que la derivada es diferenciable en todo su dominio y hay exactamente 2 valores de

x

tales que $f'(x)=0\,$ , los cuales son $x=-1\,$ y $x=4\,$ , tomando en cuenta el teorema del valor medio y que $f''(-1)<0\,$ entonces la derivada es negativa en el intervalo $(-1, 4)\,$ por lo tanto la función es decreciente en el intervalo $[-1, 4]\,$ .

Al ser una función basada en un polinomio cúbico no está acotada ni por arriba ni por abajo y como su derivada es una función cuadrática entonces no tiene más de 2 puntos con derivada igual a cero, por tanto la función es creciente en el intervalo $[4, \infty)\,$ y en el intervalo $(-\infty, -1]\,$ .