Unidad no. 7: Funciones, Límites y Continuidad.

FUNCIONES, LÌMITES Y CONTINUIDAD.

Concepto de función.

En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera depende exclusivamente del valor de la segunda. Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A = π·r². Del mismo modo, la duración T de un viaje en un tren circulando a una velocidad v de 150 km/h depende de la distancia d entre el origen y el destino: la duración es directamente proporcional a la distancia, T = d / v. A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la distancia) es la variable independiente.

Figura: Funciòn entre un conjunto de polìgonos y un conjunto de nùmeros.
A cada polìgono le corresponde su nùmero de lados.

De manera más abstracta, el concepto general de función, aplicación o mapeo se refiere en matemáticas a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto. Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero):

...	−2 → +4,	−1 → +1,	±0 → ±0,
	+1 → +1,	+2 → +4,	+3 → +9,	...

Esta asignación constituye una función entre el conjunto de los números enteros Z y el conjunto de los números naturales N. Aunque las funciones que manipulan números son las más conocidas, no son el único ejemplo: puede imaginarse una función que a cada palabra del español le asigne su letra inicial:

...,

Estación → E,

Museo → M,

Arroyo → A,

Rosa → R,

Colegio → C,

...

Esta es una función entre el conjunto de las palabras del español y el conjunto de las letras del alfabeto español.

La manera habitual de denotar una función f es:

f: A → B
a → f(a),

donde A es el dominio de la función f, su primer conjunto o conjunto de partida; y B es el codominio de f, su segundo conjunto o conjunto de llegada. Por f(a) se denota la regla o algoritmo para obtener la imagen de un cierto objeto arbitrario a del dominio A, es decir, el (único) objeto de B que le corresponde. En ocasiones esta expresión es suficiente para especificar la función por completo, infiriendo el dominio y codominio por el contexto. En el ejemplo anterior, las funciones «cuadrado» e «inicial», llámeseles f y g, se denotarían entonces como:

f: Z → N
k → k², o sencillamente f(k) = k²;
g: V → A
p → Inicial de p;

si se conviene V = {Palabras del español} y A = {Alfabeto español}.

Una función puede representarse de diversas formas: mediante el citado algoritmo para obtener la imagen de cada elemento, mediante una tabla de valores que empareje cada valor de la variable independiente con su imagen —como las mostradas arriba—, o como una gráfica que dé una imagen de la función.

Tendencia de una funciòn.

Decimos que una función

y = f (x)

tiende a un valor

y o

cuando la variable independiente x tiende a un valor $+\infty$ o $- \infty$ , si los valores de la variable $y$ se acercan a $y o$ cuando la variable

x

se acerca a dicho valor (o a $+\infty$ o $- \infty$ ).

Ejercicio: Tendencia de una función

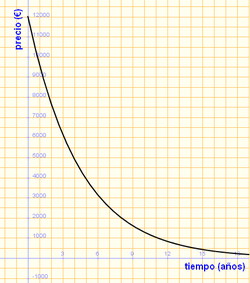
1. Compramos un coche por 12.000 €, y cada año que pasa su precio se devalua un 20%.

a) Haz una tabla que exprese el precio del coche durante los próximos 7 años.

b) Representa gráficamente los resultados del apartado a).

c) Encuentra una fórmula que exprese esta función.

d) ¿Cómo es la variable independiente: continua o discreta?

e) ¿Cuál es el dominio de esta función?. ¿Y su imagen?

f) ¿Cual es la tendencia de esta función segun pasan los años?

g) Describe el crecimiento e indica si tiene máximos o mínimos.

h) ¿Es periódica?

Solución:
a) Tabla de valores:

x	0	1	2	3	4	5	6	7
y	12.000	9.600	7.680	6.144	4.915,2	3.932,2	3.145,7	2.516,6

b) Representación gráfica:

c) 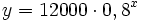$y=12000 \cdot 0,8^x \quad$ (€) d) Continua

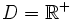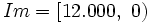e) $D=\mathbb{R}^+$ ; $Im=[12.000, \ 0)$ .

f) La función tiende a 0 a medida que transcurre el tiempo.

g) Es decreciente en todo su dominio. Tiene un máximo en

x = 0

y no tiene mínimos.

h) No es periódica.

Límite de una función.

El límite de una función es un concepto fundamental del cálculo diferencial matemático, un caso de límite aplicado a las funciones.

Informalmente, el hecho de que una función f tiene un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a c, independientemente de lo que ocurra en c.

Figura: Paràmetros utilizados en la definiciòn de lìmites.

Límites laterales

El límite cuando: x → x₀⁺ ≠ x → x₀^-. Por lo tanto, el límite cuando x → x₀ no existe.

De manera similar, x puede aproximarse a c tomando valores más grandes que éste (derecha):

$\lim_{x \to c^+}f(x) = L^+$

o tomando valores más pequeños (izquierda), en cuyo caso los límites pueden ser escritos como:

$\lim_{x \to c^-}f(x) = L^-$

Si los dos límites anteriores son iguales:

$\lim_{x \to c^-}f(x) = \lim_{x \to c^+}f(x) = L$

entonces L se pueden referir como el límite de f(x) en c. Dicho de otro modo, si estos no son iguales a L entonces el límite, como tal, no existe.

Propiedades de los límites

Si k es un escalar:

Límite de	Expresión
Una constante	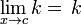$\lim_{x \to c} k =\, k\,$
La función identidad	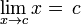$\lim_{x \to c} x = \, c \,$
El producto de una función y una constante	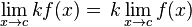$\lim_{x \to c} kf(x) =\, k\lim_{x \to c} f(x)\,$
Una suma	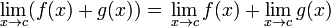$\lim_{x \to c} (f(x) + g(x)) =\, \lim_{x \to c} f(x) + \lim_{x \to c} g(x)\,$
Una resta	$\lim_{x \to c} (f(x) - g(x)) =\, \lim_{x \to c} f(x) - \lim_{x \to c} g(x)\,$
Un producto	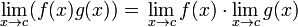$\lim_{x \to c} (f(x) g(x)) =\, \lim_{x \to c} f(x) \cdot \lim_{x \to c} g(x)\,$
Un cociente	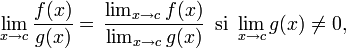$\lim_{x \to c} {{f(x)}\over {g(x)}} =\, {{\lim_{x \to c} {f(x)}} \over {\lim_{x \to c} {g(x)}}}\,\ \mbox{si } \lim_{x \to c} g(x) \ne 0,$
Una potencia	${\lim_{x \to c} f(x)^{g(x)}} =\, {\lim_{x \to c} f(x)^{\lim_{x \to c} g(x)}}\,\ \mbox{si } f(x) > 0$
Un logaritmo	${\lim_{x \to c} \log f(x)} =\, \log {\lim_{x \to c} f(x)}$
El número e	${\lim_{x \to 0} \left(1+x\right)^{1 \over x}} =\, {\lim_{x \to \infty} \left(1+{1 \over x}\right)^x } =\, e$
Función f(x) acotada y g(x) infinitesimal	${\lim_{x \to c} \left(f(x) \cdot g(x)\right)} =\, 0$ .

Indeterminaciones

Hay varios tipos de indeterminaciones, entre ellas las siguientes (considere $\infty \,\!$ como el límite que tiende a infinito y $0 \,\!$ al límite cuando tiende a 0; y no al número 0):

Operación	Indeterminación
Sustracción	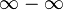$\infty - \infty$
Multiplicación	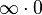$\infty \cdot 0$
División	$\cfrac{\infty}{\infty}, \cfrac{0}{0}$
Elevación a potencia	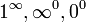$1^\infty, \infty ^0, 0^0$

Ejemplo.

0/0 es una indeterminación, es decir, no es posible, a priori, saber cual es el valor de un límite que tiende a cero sobre otro que también tiende a cero ya que el resultado no es siempre el mismo. Por ejemplo:

$\lim_{t\rightarrow 0}\frac{t}{t^2}=\infty$

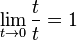
$\lim_{t\rightarrow 0}\frac{t}{t}=1$

$\lim_{t\rightarrow 0}\frac{t^2}{t}=0$

Cálculo de límites.

Veamos como tratar algunas de estas indeterminaciones. Los métodos que se indican sirven de guía en casos parecidos.

La función no está determinada para x = 1, la razón es que el denominador se hace 0. Este tipo de indeterminaciones ocurre, cuando en el numerador y el denominador de la función, existe algún factor que se hace 0, este factor suele ser del tipo : x - valor para el que queremos calcular el límite. Si logramos eliminar, este factor del numerador y del denominador, se obtiene otra función , que toma los mismos valores en todos los puntos que no sean el punto en cuestión.

En este caso concreto, el punto es : x = 1.

La nueva función permite obtener los valores en las proximidades del punto de la indeterminación, que son los que permiten calcular el límite. En el caso concreto que nos ocupa, sería:

Cuando x crece indefinidamente, esta función es un cociente de dos cantidades que crecen indefinidamente. Se puede plantear la duda, de que si al crecer x indefinidamente, también lo hará :

puesto que sería la diferencia de dos cantidades que crecen indefinidamente, que es una indeterminación. Sacando factor común se transforma esta expresión en otra equivalente:

que crece indefinidamente, puesto que una cantidad que crece indefinidamente sigue creciendo indefinidamente aunque le restemos una cantidad constante y el producto de dos cantidades que crecen indefinidamente, también crece indefinidamente. Lo mismo ocurre con el denominador.

Como, al dividir numerador y denominador por una misma cantidad, distinta de 0, el valor de la fracción no cambia, sigue que:

Esta propiedad nos permite resolver este tipo de indeterminaciones. Se divide numerador y denominador por x, elevado al mayor de los exponentes que aparece en la función :

Ejercicios resueltos.

por ùltimo Límite

Asìntota de una función.

En matemática, se le llama asíntota a una línea recta que se aproxima continuamente a otra función o curva; es decir que la distancia entre las dos tiende a cero, a medida que se extienden indefinidamente. También se puede decir que es la curva la que se aproxima continuamente a la recta; o que ambas presentan un comportamiento asintótico.

Gráfica de asíntotas

Las asíntotas ayudan a la representación de curvas, proporcionan un soporte estructural e indican su comportamiento a largo plazo. En tanto que líneas rectas, la ecuación de una asíntota es simplemente la de una recta, y su expresión analítica dependerá de la elección del sistema de referencias (y = m•x + b en coordenadas cartesianas).

Si bien suelen representarse en un mismo sistema de coordenadas, las asíntotas no forman parte de la expresión analítica de la función, por lo que -en numerosos ejemplos- no están incluidas explícitamente dentro de la gráfica, o bien se las indica con una línea punteada. En muchos casos, las asíntotas coinciden con los ejes de coordenadas, es decir que sus ecuaciones en coordenadas cartesianas serán: x = 0, y = 0.

Se distinguen tres tipos:

Asíntotas verticales: rectas perpendiculares eje de las abscisas, de ecuación x = c^te.

Asíntotas horizontales: rectas perpendiculares al eje de las ordenadas, de ecuación y = c^te.

Asíntotas oblicuas: si no son paralelas o perpendiculares a los ejes, de ecuación y = m•x + b.

(Nota: c^te=constante).

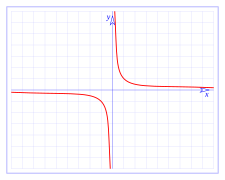Continuidad de una función.

En matemáticas, una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Si la función no es continua, se dice que es discontinua. Generalmente una función continua es aquella cuya gráfica puede dibujarse sin levantar el lápiz del papel.

La continuidad de funciones es uno de los conceptos principales de la topología. El artículo describe principalmente la continuidad de funciones reales de una variable real.

Funciones reales de una variable real

Informalmente hablando, una función f definida sobre un intervalo I es continua si la curva que la representa, es decir el conjunto de los puntos (x, f(x)), con x en I, está constituida por un trazo continuo, es decir un trazo que no está roto, ni tiene "hoyos" ni "saltos", como en la figura de arriba.

El intervalo I de x es el dominio de definición de f, definido como el conjunto de los valores de x para los cuales f(x) existe.

El intervalo J de y es el rango (también conocido como imagen) de f, el conjunto de los valores de y, tomados como y = f(x). Se escribe J = f(I). Notar que en general, no es igual que el codominio (sólo es igual si la función en cuestión es suprayectiva.)

El mayor elemento de J se llama el máximo absoluto de f en I, y el menor valor de J es su mínimo absoluto en el dominio I.

Minaya - CCR

Datos personales