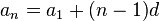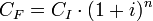Sucesiones de números.
Definiciones:
- Una sucesión de números es un conjunto de infinitos números ordenados:
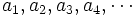
- Cada uno de los números que componen la sucesión se llaman términos de la sucesión. Se nombran con una letra y un subíndice que depende del lugar que el término ocupa en la sucesión.
- A veces, podemos encontrar una expresión (fórmula) que sirve para obtener un término cualquiera de la sucesión con solo saber el lugar que este ocupa. A esta expresión se le llama término general.
Ejemplo: Sucesión
Dada la sucesión
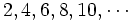
- a) Halla el término 10.
- b) Halla el término general.
En esta sucesión, los términos son:
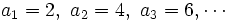 .
. El término que ocupa el décimo lugar se designará por  , que en este caso es el 20.
, que en este caso es el 20.
 , que en este caso es el 20.
, que en este caso es el 20. El término general de esta sucesión es 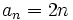 porque cada término se obtiene multiplicando la posición que ocupa por 2.
porque cada término se obtiene multiplicando la posición que ocupa por 2.
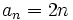 porque cada término se obtiene multiplicando la posición que ocupa por 2.
porque cada término se obtiene multiplicando la posición que ocupa por 2. 1. Escribe los cinco primeros términos de la sucesión cuyo primer término es 2 y todos los demás se obtienen sumando 5 al término anterior.
Soluciòn:
2,7,12,17,22,27....
2. El término general de una sucesión es
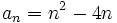 . Calcula los cinco primeros términos y
. Calcula los cinco primeros términos y  :
: Soluciòn:
-3,-4,-3,0 y 5.
a10 = 102 − 4.10 = 60
3. Intenta escribir una expresión que sirva para calcular cualquier término de las sucesiones siguientes:
a) 1,2,3,4,5,... b) 1,4,9,16,... c) 1,3,5,7,...
d) 1/2,1/4,1/8,... e) -1,1,-1,1,-1,... f) 1,-1,1,-1,1,... Soluciòn:
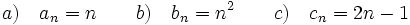

Clasificación de sucesiones:
Sucesión finita
Diremos que una sucesión es finita si determinamos su último término, por ejemplo el n-ésimo: Genéricamente:  , donde
, donde  sería el término general si hiciese falta.
sería el término general si hiciese falta.
 , donde
, donde  sería el término general si hiciese falta.
sería el término general si hiciese falta. Ejemplo: 100, 99, 98, ... , 1, 0.
Sucesión constante
Diremos que una sucesión es constante si todos los términos valen un mismo valor,  , es decir, un mismo número real cualquiera, ejemplo: Genéricamente
, es decir, un mismo número real cualquiera, ejemplo: Genéricamente  Ejemplo: si
Ejemplo: si  queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1.
queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1.
 , es decir, un mismo número real cualquiera, ejemplo: Genéricamente
, es decir, un mismo número real cualquiera, ejemplo: Genéricamente  Ejemplo: si
Ejemplo: si  queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1.
queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1. Sucesión creciente
Si imponemos al término general, de una sucesión numérica, la condición que  , es decir, que el siguiente término,
, es decir, que el siguiente término,  , siempre sea mayor estricto que su predecesor,
, siempre sea mayor estricto que su predecesor,  , se llaman sucesiones estrictamente crecientes:
, se llaman sucesiones estrictamente crecientes:
 , es decir, que el siguiente término,
, es decir, que el siguiente término,  , siempre sea mayor estricto que su predecesor,
, siempre sea mayor estricto que su predecesor,  , se llaman sucesiones estrictamente crecientes:
, se llaman sucesiones estrictamente crecientes: - Para naturales: 1, 2, 3, 4, 5, 6, ... .
- Para enteros: -10, -9, -8, -7, -6, ... .
- Para reales:
 .
.
Si imponemos  , es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.
, es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.
 , es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.
, es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes. Sucesión decreciente
Al igual que las crecientes tenemos, según el término general, que:
Si  entonces la sucesión es decreciente
entonces la sucesión es decreciente
Si  es estrictamente decreciente.
es estrictamente decreciente.
 es estrictamente decreciente.
es estrictamente decreciente. Sucesión alternada
Intuitivamente se llama sucesión alternada cuando alterna valores de signo opuesto, como an = ( − 1)n que nos genera la sucesión: a0=1, -1, 1, -1, 1, -1, ... . Utilizada por las series llamadas series alternadas.
Cotas de una sucesiòn.
Sucesiones Acotadas Inferiormente
Se dice que una sucesión de números reales esta acotada inferiormente si hay un número k menor que todos los términos de la sucesión. Es decir que todos los términos de la sucesión son siempre mayores que k.
Por lo tanto, en su representación en el plano cartesiano los puntos estarán por encima de la recta y = k.
an ≥ k
Sucesiones Acotadas Superiormente
Se dice que una sucesión de números reales esta acotada superiormente si hay un número K mayor que todos los términos de la sucesión. Es decir que todos los términos de la sucesión son siempre menores que K.
Por lo tanto, su representación en el plano cartesiano serán puntos que no sobrepasan la recta y = K.
an ≤ K
Sucesiones Acotadas
Se dice que una sucesión de números reales está acotada si está acotada superiormente e inferiormente. Es decir si hay un número k menor que todos los términos de la sucesión y otro K mayor que todos los términos de la sucesión. Es decir que todos los términos de la sucesión están comprendidos entre k y K.
Por lo tanto, en su representación en el plano cartesiano los puntos estarán entre la recta y = k y la recta y = K.
Sucesiones No Acotadas
Se dice que una sucesión de números reales no está acotada si no lo está superiormente o inferiormente, es decir cuando no está acotada por alguno de los dos lados o por ambos a la vez.
Operaciones con sucesiones.
Dadas las sucesiones an y bn:
an= a1, a2, a3, ..., an
bn= b1, b2, b3, ...,bn
Suma de sucesiones:
(an) + (bn) = (an + bn)
(an) + (bn) = (a1 + b1, a2 + b2, a3 + b3, ..., an + bn)
Diferencia de suceciones:
(an) - (bn) = (an - bn)
(an) - (bn) = (a1 - b1, a2 - b2, a3 - b3, ..., an - bn)
Producto de suceciones:
(an) · (bn) = (an · bn)
(an) · (bn) = (a1 · b1, a2 · b2, a3 · b3, ..., an · bn)
Sucesiòn Inversible:
Una sucesión es inversible o invertible si todos sus términos son distintos de cero. Si la sucesión bn es inversible, su inversa es:

Cociente de suceciones:
Sólo es posible el cociente entre dos sucesiones si el denominador es inversible.
bn= b1, b2, b3, ...,bn
Suma de sucesiones:
(an) + (bn) = (an + bn)
(an) + (bn) = (a1 + b1, a2 + b2, a3 + b3, ..., an + bn)
Diferencia de suceciones:
(an) - (bn) = (an - bn)
(an) - (bn) = (a1 - b1, a2 - b2, a3 - b3, ..., an - bn)
Producto de suceciones:
(an) · (bn) = (an · bn)
(an) · (bn) = (a1 · b1, a2 · b2, a3 · b3, ..., an · bn)
Sucesiòn Inversible:
Una sucesión es inversible o invertible si todos sus términos son distintos de cero. Si la sucesión bn es inversible, su inversa es:

Cociente de suceciones:
Sólo es posible el cociente entre dos sucesiones si el denominador es inversible.
SERIES.
En matemáticas, una serie es la generalización de la noción de suma a los términos de una sucesión infinita. Informalmente, es el resultado de sumar los términos: a1 + a2 + a3 + · · lo cual suele escribirse en forma más compacta con el símbolo de sumatoria: 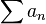 .
.
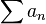 .
.El estudio de las series consiste en la evaluación de la suma de un número finito n de términos sucesivos, y mediante un pasaje al límite identificar el comportamiento de la serie a medida que n crece indefinidamente.
Una secuencia o cadena «finita», tiene un primer y último término bien definidos; en cambio en una serie infinita, cada uno de los términos suele obtenerse a partir de una determinada regla o fórmula, o por algún algoritmo. Al tener infinitos términos, esta noción suele expresarse como serie infinita, pero a diferencia de las sumas finitas, las series infinitas requieren de herramientas del análisis matemático para ser debidamente comprendidas y manipuladas. Existe una gran cantidad de métodos para determinar la naturaleza de convergencia o no-convergencia de las series matemáticas, sin realizar explícitamente los cálculos.
Progresiones aritméticas.
En matemáticas, una progresión aritmética es una suceciòn de números tales que la diferencia de dos términos sucesivos cualesquiera de la secuencia es una constante, cantidad llamada diferencia de la progresión o simplemente diferencia o incluso "distancia".
Por ejemplo, la sucesión 3, 5, 7, 9, 11,... es una progresión aritmética de constante (o diferencia común) 2.
Término general de una progresión aritmética
El término siguiente de una progresión aritmética es aquel que se obtiene sumándole la diferencia al término anterior. El término general de una progresión aritmética es la expresión que nos da cualquiera de sus términos, conocidos alguno de ellos y la diferencia de la progresión. La fórmula del término general de una progresión aritmética es:
Donde d es un número real llamado diferencia. Si el término inicial de una progresión aritmética es  y la diferencia común es
y la diferencia común es  , entonces el término
, entonces el término  -ésimo de la sucesión viene dada por
-ésimo de la sucesión viene dada por
 y la diferencia común es
y la diferencia común es  , entonces el término
, entonces el término  -ésimo de la sucesión viene dada por
-ésimo de la sucesión viene dada por  , n = 0, 1, 2,... si el término inicial se toma como el cero.
, n = 0, 1, 2,... si el término inicial se toma como el cero. n = 1, 2, 3,... si el término inicial se toma como el primero.
n = 1, 2, 3,... si el término inicial se toma como el primero.
La primera opción ofrece una fórmula más sencilla, pero emplea una terminología más confusa, ya que no es común en el lenguaje el uso de "cero" como ordinal. Generalizando, sea la progresión aritmética:
de diferencia

tenemos que
- ...
sumando miembro a miembro todas esas igualdades, y simplificando términos semejantes, obtenemos:
(I)
Expresión del término general de la progresión, conocidos su primer término y la diferencia. Pero también podemos escribir el término general de otra forma.Para ello consideremos los términos  y
y  (
( ) de la progresión anterior y pongámolos en función de
) de la progresión anterior y pongámolos en función de  :
:
 y
y  (
( ) de la progresión anterior y pongámolos en función de
) de la progresión anterior y pongámolos en función de  :
: Restando ambas igualdades, y trasponiendo, obtenemos:
(II)
Expresión más general que (I) pues nos da los términos de la progresión conociendo uno cualquiera de ellos, y la diferencia.
Dependiendo de que la diferencia  de una progresión aritmética sea positiva, nula o negativa, tendremos:
de una progresión aritmética sea positiva, nula o negativa, tendremos:
 de una progresión aritmética sea positiva, nula o negativa, tendremos:
de una progresión aritmética sea positiva, nula o negativa, tendremos: - d>0: progresión creciente. Cada término es mayor que el anterior.
- Ejemplo: 3, 6, 9, 12, 15, 18... (d = 3)
- d=0: progresión constante. Todos los términos son iguales.
- Ejemplo: 2, 2, 2, 2, 2... (d = 0)
- d<0: progresión decreciente. Cada término es menor que el anterior.
- Ejemplo: 5, 3, 1, -1, -3, -5, -7... (d = − 2)
Suma de todos los términos de una progresión aritmética
La suma de los términos en un segmento inicial de una sucesión aritmética se conoce a veces como serie aritmética. Existe una fórmula para las series aritméticas. La suma de los n primeros valores de una sucesión finita viene dada por la fórmula:
donde a1 es el primer término y an el último.
Progresiones geométricas.
Una progresión geométrica está constituida por una secuencia de elementos en la que cada uno de ellos se obtiene multiplicando el anterior por una constante denominada razón o factor de la progresión. Se suele reservar el término progresión cuando la secuencia tiene una cantidad finita de términos mientras que se usa sucesión cuando hay una cantidad infinita de términos, si bien, esta distinción no es estricta.
Así,  es una progresión geométrica con razón igual a 3, porque:
es una progresión geométrica con razón igual a 3, porque:
 es una progresión geométrica con razón igual a 3, porque:
es una progresión geométrica con razón igual a 3, porque: - 15 = 5 × 3
- 45 = 15 × 3
- 135 = 45 × 3
- 405 = 135 × 3
y así sucesivamente.
Aunque es más fácil aplicando la fórmula:
Siendo  el término en cuestión,
el término en cuestión,  el primer término y
el primer término y  la razón:
la razón:
 el término en cuestión,
el término en cuestión,  el primer término y
el primer término y  la razón:
la razón: Así quedaría si queremos saber el sexto término de nuestra progresión:
Ejemplos de progresiones geométricas
La progresión 1, 2 ,4 ,8 ,16, es una progresión geométrica cuya razón vale 2, al igual que 5, 10, 20, 40.
La razón no necesariamente tiene que ser un número entero. Así, 12, 3, 0.75, 0.1875 es una progresión geométrica con razón 1/4.
La razón tampoco tiene por qué ser positiva. De este modo la progresión 3, -6, 12, -24 tiene razón -2. Este tipo de progresiones es un ejemplo de progresión alternante porque los signos alternan entre positivo y negativo.
Cuando la razón es igual a 1 se obtiene una progresión constante: 7, 7, 7, 7
Un caso especial es cuando la razón es igual a cero, por ejemplo: 4, 0, 0, 0. Existen ciertas referencias que no consideran este caso como progresión y piden explícitamente que  en la definición.
en la definición.
 en la definición.
en la definición. Suma de los primeros n términos de una progresión geométrica
Se denomina como Sn a la suma de n términos consecutivos de una progresión geométrica:
- Ejercicios resueltos.1. En las siguientes progresiones aritméticas, calcula el término general de cada una de ellas.a) 1, -1, -3, -5, -7,.... b) 2, 5, 8, 11, 14,.... c) -7, -5, -3, -1, 1,... Soluciòn:
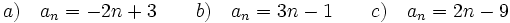 2. Si
2. Si 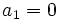 y
y 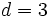 , en una progresión aritmética, ¿cuánto vale
, en una progresión aritmética, ¿cuánto vale 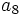 ? Soluciòn:
? Soluciòn: 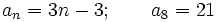 3. Si
3. Si 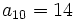 y
y 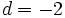 , calcular
, calcular 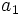 . Soluciòn:
. Soluciòn: 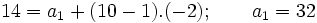 4. En las siguientes progresiones geométricas, calcula el término general de cada una de ellas.a) 1, 3, 9, 27.... b) 4, -4, 4, -4,.... c) 27, 9, 3, 1,... Soluciòn:
4. En las siguientes progresiones geométricas, calcula el término general de cada una de ellas.a) 1, 3, 9, 27.... b) 4, -4, 4, -4,.... c) 27, 9, 3, 1,... Soluciòn: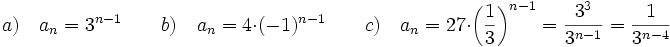 5. ¿Cuál es la razón de una progresión geométrica cuyo primer término es 2 y el cuarto término 250? Soluciòn:
5. ¿Cuál es la razón de una progresión geométrica cuyo primer término es 2 y el cuarto término 250? Soluciòn: 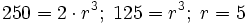 Porcentajes.En matemáticas, un porcentaje es una forma de expresar un número como una fracción de 100 por ciento,( que significa “de cada 100”). Es a menudo denotado utilizando el signo porcentaje %, que se debe escribir inmediatamente después del número al que se refiere, sin dejar espacio de separación.1 Por ejemplo: "treinta y dos por ciento" se representa mediante 32% y significa 'treinta y dos de cada cien'. También puede ser representado como 32 / 100El símbolo % es una forma estilizada de los dos ceros. Evolucionó a partir de un símbolo similar sólo que presentaba una línea horizontal en lugar de diagonal (c. 1650), que a su vez proviene de un símbolo que representaba "P cento" (c.1425).El porcentaje es un tanto por ciento (cien unidades), por lo que se concluye que es una cantidad que corresponde proporcionalmente a una parte de cien.
Porcentajes.En matemáticas, un porcentaje es una forma de expresar un número como una fracción de 100 por ciento,( que significa “de cada 100”). Es a menudo denotado utilizando el signo porcentaje %, que se debe escribir inmediatamente después del número al que se refiere, sin dejar espacio de separación.1 Por ejemplo: "treinta y dos por ciento" se representa mediante 32% y significa 'treinta y dos de cada cien'. También puede ser representado como 32 / 100El símbolo % es una forma estilizada de los dos ceros. Evolucionó a partir de un símbolo similar sólo que presentaba una línea horizontal en lugar de diagonal (c. 1650), que a su vez proviene de un símbolo que representaba "P cento" (c.1425).El porcentaje es un tanto por ciento (cien unidades), por lo que se concluye que es una cantidad que corresponde proporcionalmente a una parte de cien.El tanto por ciento como fracción
El tanto por ciento se divide entre 100 y se simplifica la fracción. Ejemplo:Para saber como se representa el 10% en fracción se divide y luego se simplifica:Obtener un tanto por ciento de un número
Para obtener un tanto por ciento se construye una regla de tres simple. Ejemplo:Para calcular el 25% de 150 se hace la regla de tres: multiplica cruzado y divide por el que queda solo.Por tanto: 37.5 es el 25% de 150
Interés simple.
Su fórmula está dada por:

Despejando las variables Capital, Tasa y Tiempo se obtiene:

![i = \left [ \frac{I_s}{C_I \cdot t} \right ] \times 100](http://upload.wikimedia.org/wikipedia/es/math/4/5/0/4504118643018f4b669d8c7525d51e43.png)

Donde:
IS: Es el interés Simple
CI: Es el Capital Inicial
i: Es la tasa de interés expresada en tanto por uno, que al ser multiplicada por 100, quedará expresada en tanto por ciento.
t: Es el tiempo expresado en años.
Interés compuesto.
El interés compuesto representa el costo del dinero, beneficio o utilidad de un capital Inicial (CI) o principal a una tasa de interés (i) durante un período (t),en el cual los intereses que se obtienen al final de cada período de inversión no se retiran sino que se reinvierten o añaden al capital inicial, es decir, se capitalizan.
Cálculo del interés compuesto
Para un período de tiempo determinado, el capital final (CF) se calcula con base a la fórmula
Ahora, capitalizando el valor obtenido en un segundo período
Repitiendo esto para un tercer período
y generalizando a n períodos, se obtiene la fórmula de interés compuesto:
donde:
 es el capital final en el n-ésimo período;
es el capital final en el n-ésimo período; es el capital inicial;
es el capital inicial; interés del período y
interés del período y el número de períodos
el número de períodos- Ejercicios resueltos.1. Calcular el interés simple cobrado por un préstamo de $10,000.00 a una tasa del 6% anual.Soluciòn: CI = 10000 ; i = 6% ; t = 1 añoIs = CI . i . tIs = 10000*6%*1 = 10000*0.06*1Is = 600Esto quiere decir que al final del año se debe pagar un interés de $600.002.Una persona comprò una radio en $79.95, dio un anticipo de $19.95 y acordó pagar el resto en 3 meses, mas un cargo adicional de $2. ¿Qué tasa de interés simple pagó?. Soluciòn: Con la opción de que pagò $2 de interés, sobre 79.95 - 19.95 = $60.00, por tres meses, tenemos que: CI = 60, Is = 2, t = 1/4. Aplicando Is = CI.i.t 2 = 60 (i) (1/4) = 15i i = 2/15 = 0.13333 = 13 %