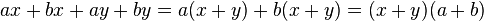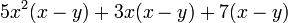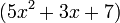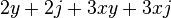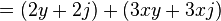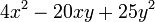Unidad no. 1: Expresiones Algebraicas.

EXPRESIONES ALGEBRAICAS

Concepto de Expresiones Algebraicas

Una expresión algebraica es una combinación de letras, números y signos de operaciones aritmèticas. Las letras suelen representar cantidades desconocidas y se denominan variables o incógnitas. Las expresiones algebraicas nos permiten traducir al lenguaje matemático expresiones del lenguaje habitual.

Ejemplo: Expresión algebraica

Expresa el Perímetro y el Àrea de un terreno rectangular.

Si suponemos que mide X metros de largo y Y metros de ancho, tenemos que:

Perìmetro = 2X + 2Y
Àrea = X . Y

Definiciones:

Monomio: Es una expresión algebraica en la que las ùnicas operaciones que aparecen son la multiplicaciòn y la potenciaciòn de exponente natural.

Ejemplo 1 : 3XY³Z²

El grado de un monomio respecto de una variable es el exponente a que està elevada dicha variable. Si el monomio tiene varias variables, su grado total es la suma de los grados de todas sus variables. En el ejemplo 1, el grado es igual a 6.

Polinomio: Es una expresiòn algebraica formada por la suma o diferencia de varios monomios.

Ejemplo 2 : 2X³ + 3X² - 2X + 1

Cada uno de los monomios que componen el polinomio se denomina Tèrmino.

Los Coeficientes de las variables son los nùmeros reales que aparecen delante de ellas en cada tèrmino.

El grado de un polinomio es el del tèrmino de mayor grado, que se denomina tèrmino Principal. En el ejemplo 2, el grado es igual a 3.

El tèrmino de grado cero se denomina tèrmino Independiente.

Tèrminos semejantes: Son aquellos que contienen las mismas variables elevadas a igual exponente y solo varìan en sus coeficientes.

Polinomios Completos: Son los que contienen todos los grados de la variable, desde el mayor hasta cero y viceversa, o desordenados ( ejemplo no. 2 ).

Valor numèrico de un polinomio: Es el valor que resulta cuando sustituimos las variables de un polinomio por un determinado nùmero real.

Ejemplo 3 : Hallar el valor numèrico del polinomio 5X³ - X² + 3X - 2, para X = - 2:

Se sustituye X por - 2:
5(-2)³ - (-2)² + 3(-2) - 2 =

5(-8) - (4) - 6 - 2 =

- 40 - 4 - 6 - 2 = - 52.

Raices de un polinomio: Se denomina raìz a cualquier valor de la variable para el cual el valor numèrico del polinomio es cero. Un polinomio tendrà el nùmero de raices que indique su grado.

Ejemplo 4 : Encontrar el valor numèrico del polinomio X³ + X + 30 , para X = - 3:

Sustituyendo X por - 3:
(-3)³ + (-3) + 30 =

- 27 - 3 + 30 = 0

Luego -3 es una de las tres raices del polinomio X³ + X + 30.

Operaciones con polinomios.

Suma de polinomios: La suma de dos polinomios es otro polinomio que se obtiene sumando los tèrminos semejantes y dejando indicada la suma de los no semejantes.

Ejemplo: Dados los polinomios P(x) = -2x³ + 3x² - x + 5 y Q(x) = 5x⁴ + 2x² + 4x - 3, realice la suma de P(x) + Q(x):

-2x³ + 3x² - x + 5
5x⁴ + 2x² + 4x - 3
5x⁴ -2x³+5x² +3x + 2

Resta o Diferencia de polinomios: Esta se realiza de igual forma que la suma, pero antes de sumar se le cambia el signo al sustraendo.

Ejemplo: Dados los polinomios P(x) = -2x³ + 3x² - x + 5 y Q(x) = 5x⁴ + 2x² + 4x - 3, realice la resta de P(x) - Q(x):

El sustraendo es Q(x).

-Q(x) = -5x⁴ - 2x² - 4x + 3

Ahora podemos sumar:

-2x³ + 3x² - x + 5

-5x⁴ - 2x² - 4x + 3

-5x⁴-2x³ + x² - 5x + 8

Multiplicaciòn o producto de polinomios: El producto de dos polinomios es otro polinomio que se obtiene multiplicando tèrmino a tèrmino, aplicando la propiedad distributiva y simplificando despuès los tèrminos semejantes.

Ejemplo: Realiza la multiplicaciòn de los polinomios siguientes:

(2x³ - 3x + 5).(4x² - 2) =

Multiplicamos primero 4x² (primer tèrmino del segundo factor) por el primer factor, luego hacemos lo mismo con -2 (ùltimo tèrmino del segundo factor) y colocamos semejantes debajo de semejantes para realizar la suma:

2x³ - 3x + 5
____4x² -2_____________

8x⁵ -12x³ + 20x²

___ - 4x³ +6x - 10

8x⁵ - 16x³ +20x² +6x -10

Divisiòn de polinomios: Para dividir dos polinomios se realiza el siguiente proceso:

1^ro Se ordena y completa el polinomio dividendo.

2^do Se divide el primer tèrmino del dividendo entre el primero del divisor(èste debe estar ordenado).

3^ro Se multiplica el tèrmino obtenido (Primero del cociente) por todos los tèrminos del divisor y se resta al dividendo. Para ello se cambia el signo y se suma.

4^to Se repite el proceso hasta obtener un resto o residuo de grado menor que el divisor.

Ejemplo: Realiza la divisiòn (-7x³ + 7 + 3x⁴ + 12x²) ÷ (3x² - x + 1)

El dividendo ordenado y completo es: 3x⁴ - 7x³ + 12x² + 0x + 7

Ahora podemos dividir:

3x⁴ - 7x³ + 12x² + 0x + 7 ¦3x² - x + 1__

-3x⁴ + x³ - x²_____ x² - 2x + 3 → Cociente

-6x³ + 11x² + 0x

6x³ - 2x² + 2x_____
9x² + 2x + 7

-9x² + 3x - 3__

5x + 4 → Resto

Regla de Ruffini (Divisiòn Sintética)

En las divisiones de polinomios en las que el divisor es un binomio de la forma x ± a,donde a es un nùmero real cualquiera, diferente de cero, se puede aplicar la Regla de Ruffini para obtener el cociente y el resto.

Ejemplo: Realiza la divisiòn (3x³ + 4x - 6) ÷ (x + 2).

1^ro Se escriben los coeficientes del dividendo ordenado y completo, si faltan grados de la variable se pone cero en su lugar. A la izquierda se escribe el valor a, en este caso -2 (tèrmino independiente del divisor cambiado de signo, esto es, la raìz del divisor).

¦ 3 0 4 -6

-2¦____________________

2^do Se baja el primer coeficiente del dividendo (3), se multiplica por -2, se escribe el resultado debajo del segundo coeficiente del dividendo (0) y se suma a este.

¦ 3 0 4 -6

-2¦_____-6_____________

¦ 3 -6

3^ro Se multiplica el -6 obtenido de la suma por -2, se escribe el resultado debajo del tercer coeficiente del dividendo (4) y se suma a este.

¦ 3 0 4 -6

-2¦____-6____12________

¦ 3 -6 16

4^to Se repite el proceso hasta llegar al ùltimo coeficiente del dividendo.

¦ 3 0 4 - 6

-2¦____ -6___12___-32_____

¦ 3 -6 16 -38 → Resto

5^to El ùltimo nùmero obtenido de la suma es el resto (-38), y los anteriores son los coeficientes ordenados del polinomio cociente, cuyo grado es inferior en una unidad al del dividendo:

3x² - 6x + 16 → Cociente

Teoremas del Resto y del Factor

Teorema del Resto: Al dividir un polinomio P(x) entre un binomio x ± a, el resto que se obtiene es igual al valor numèrico del polinomio en x =-a.

Ejemplo: Encontrar el resto de la división de (x³ + 2x² - 5x - 6) ÷ (x + 3) y luego compararlo con el valor numèrico para x = -3:

¦ 1 2 -5 -6

-3 ¦__ -3____3___6____

¦ 1 -1 -2 0 → Resto

Si sustituimos el valor x = -3, en el polinomio x³ + 2x² - 5x - 6, resulta:
(-3)³ + 2(-3)² - 5(-3) - 6 =
-27 + 2(9) + 15 - 6 =
-27 + 18 + 15 - 6 = 0
Por tanto, queda demostrado.

Teorema del Factor: Si x = -a es una raìz de un polinomio, entonces èste es divisible entre x+a, es decir, x + a es un factor del polinomio y la divisiòn es exacta.
Ejemplo: En la divisiòn anterior el polinomio cociente es x² - x - 2, si lo multiplicamos por x + 3, debe dar como resultado el polinomio dividendo:
x² - x - 2
x + 3
x³ - x² - 2x
3x² - 3x - 6
x³ + 2x² - 5x - 6
Por tanto, queda demostrado.

Factorizaciòn de Polinomios.

En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores). En el caso de números debemos utilizar los números primos, que al multiplicarlos todos, resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y a² - b² se factoriza como binomios conjugados (a - b)(a + b).

Caso I - Factor común

Sacar el factor común es añadir la literal común de un polinomio, binomio o trinomio, con el menor exponente y el divisor común de sus coeficientes, y expresarlo como el producto de dos factores.

Factor común monomio

Factor común por agrupación de términos

$ab + ac + ad = a ( b + c + d) \,$

$ax + bx + ay + by = a (x+y) + b (x+y) = (x+y)(a + b ) \,$

Factor común polinomio

Primero hay que determinar el factor común de los coeficientes junto con el de las variables (la que tenga menor exponente). Se toma en cuenta aquí que el factor común no solo cuenta con un término, sino con dos.

Ejemplo:

$5x^2(x-y) + 3x(x-y) +7(x-y) \,$

Se aprecia claramente que se está repitiendo el polinomio (x - y), entonces ese será el factor común. El otro factor será simplemente lo que queda del polinomio original, es decir:

$(5x^2 + 3x +7) \,$

La respuesta es:

$(5x^2+3x+7)(x-y) \,$

En algunos casos se debe utilizar el número 1, por ejemplo:

$5a^2(3a+b) +3a +b \,$

Se puede utilizar como:

$5a^2(3a+b) + 1(3a+b) \,$

Entonces la respuesta es:

$(3a+b) (5a^2+1) \,$

Caso II - Factor común por agrupación de términos

Para trabajar un polinomio por agrupación de términos, se debe tener en cuenta que son dos características las que se repiten. Se identifica porque es un número par de términos.

Un ejemplo numérico puede ser:

$2y + 2j +3xy + 3xj\,$

entonces puedes agruparlos de la siguiente manera:

$= (2y+2j)+(3xy+3xj)\,$

Aplicamos el caso I (Factor común)

$= 2(y+j)+3x(y+j)\,$

$= (2+3x)(y+j)\,$

Caso III - Trinomio Cuadrado Perfecto

Se identifica por tener tres términos, de los cuales dos tienen raíces cuadradas exactas, y el restante equivale al doble producto de las raíces del primero por el segundo. Para solucionar un Trinomio Cuadrado Perfecto debemos reordenar los términos dejando de primero y de tercero los términos que tengan raíz cuadrada, luego extraemos la raíz cuadrada del primer y tercer término y los escribimos en un paréntesis, separándolos por el signo que acompaña al segundo término, al cerrar el paréntesis elevamos todo el binomio al cuadrado o lo escribimos dos veces.

$(a-b)^2 = a^2-2ab+b^2\,$

Ejemplo 1:

$(5x-3y)^2 = 25x^2-30xy+9y^2\,$

Ejemplo 2:

$(3x+2y)^2 = 9x^2+12xy+4y^2\,$

Ejemplo 3:

$(x+y)^2 = x^2+2xy+y^2\,$

Ejemplo 4:

$4x^2+25y^2-20xy\,$

Organizando los términos tenemos

$4x^2 - 20xy + 25y^2\,$

Extrayendo la raíz cuadrada del primer y último término y agrupándolos en un paréntesis separados por el signo del segundo término y elevando al cuadrado nos queda:

$(2x - 5y)^2\,$

Al verificar que el doble producto del primero por el segundo término es -20xy determinamos que es correcta la solución. De no ser así, esta solución no aplicaría.

Caso IV - Diferencia de cuadrados

Se identifica por tener dos términos elevados al cuadrado y unidos por el signo menos. Se resuelve por medio de dos paréntesis, parecido a los productos de la forma (a - b)(a + b), uno negativo y otro positivo.

$(ay)^2-(bx)^2= (ay-bx)(ay+bx)\,$

Ejemplo:

$9y^2-4x^2= (3y)^2-(2x)^2= (3y+2x)(3y-2x)\,$

Caso V - Trinomio de la forma x² + bx + c

Se identifica por tener tres términos, hay una literal con exponente al cuadrado y uno de ellos es el término independiente. Se resuelve por medio de dos paréntesis, en los cuales se colocan la raíz cuadrada de la variable, el signo del primer factor es el del segundo tèrmino y el del segundo el resultado del producto del signo del segundo tèrmino por el del tercero, y buscando dos números que multiplicados den como resultado el término independiente y sumados o restados, den como resultado el coeficiente del segundo término. Cuando los factores tengan igual signo se suman los nùmeros buscados y cuando los factores tengan signos diferentes se restan los nùmeros buscados y se escribe el mayor en el primer factor.

Ejemplo 1:

$a^2+2a-15 = (a+5) (a-3) \,$

Ejemplo 2:

$x^2+5x+6 = (x+3)(x+2)\,$

Caso VI - Trinomio de la forma ax² + bx + c

En este caso se tienen 3 términos: El primer término tiene un coeficiente distinto de uno, la letra del segundo término tiene la mitad del exponente del término anterior y el tercer término es un término independiente, o sea sin una parte literal, así:

$4x^2+12x+9\,$

Para factorizar una expresión de esta forma, se multiplica el término independiente por el coeficiente del primer término(4x²) :

$4x^2+12x+(9\cdot4)\$

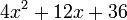
$4x^2+12x+36\,$

Luego debemos encontrar dos números que multiplicados entre sí den como resultado el término independiente y que su suma sea igual al coeficiente del término x :

$6\cdot6=36$

$6+6=12\,$

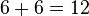
Después procedemos a colocar de forma completa el término x² sin ser elevado al cuadrado en paréntesis, además colocamos los 2 términos descubiertos anteriormente :

$(4x+6)(4x+6)\,$

Para terminar dividimos estos términos por el coeficiente del término x² :

$\frac{(4x+6)(4x+6)}{4}\,$ : $=\frac{(4x+6)}{2}\cdot \frac{(4x+6)}{2}\,$

Queda así terminada la factorización :

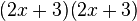$(2x+3)(2x+3)\,$ : $=(2x+3)^2\,$

Minaya - CCR

Datos personales